B3-1: The Moment of Inertia of a Cylinder

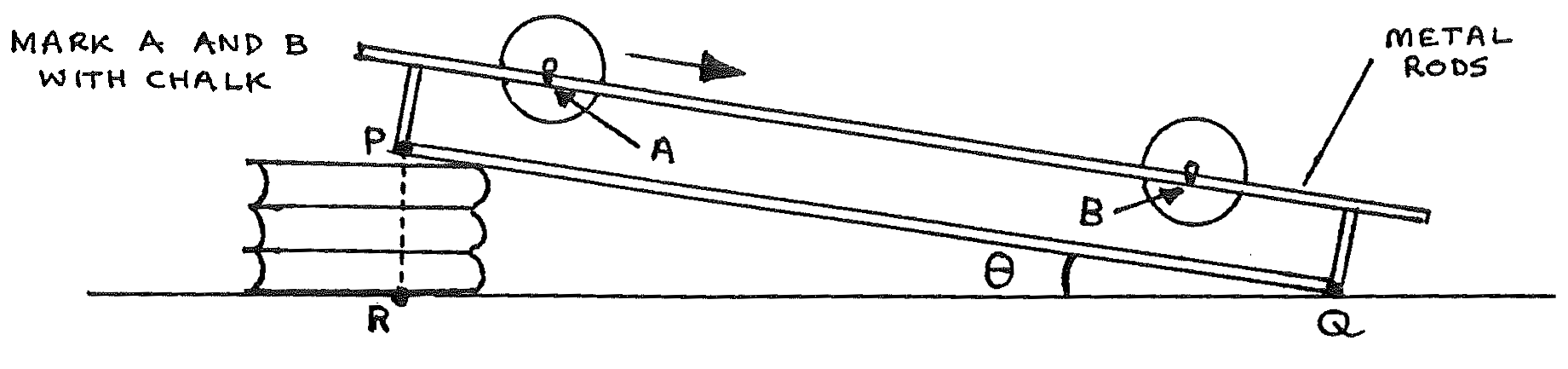
Apparatus

2 mounted rails; 2 different cylinders with axles; metre rule; micrometer screw gauge; stack of books; stop watch; piece of chalk; triple beam balance; graph paper

Procedure

1. Set up the apparatus as shown above with $PR$ less than $4\text{cm}$. Measure $s=AB$ and measure $PQ$. Record $s$ and $PQ$.
2. Measure and record $PR$. Calculate $\sin\theta = \frac{PR}{PQ}$.
3. Place a cylinder at $A$. Record the time, $t$, for the cylinder, starting from rest, to roll from $A$ to $B$.
4. Determine the linear acceleration, $a$, of the cylinder using your readings of $s$ and $t$.
5. Increase $PR$ and repeat steps 2, 3, and 4. Increase $PR$ three more times, repeating steps 2, 3, and 4 to obtain five sets of readings.
6. Measure the axle diameter and find the axle radius, $r_a$. Find the cylinder radius, $r$. Measure the mass, $M$, of the cylinder and axle.
7. Repeat steps 2 to 6 for the second cylinder.

Observations

For each cylinder:

$M$ = ________kg

$r_a$ = ________m

$r$ = ________m

Tabulate:

Theory

The cylinder loses potential energy ($PE$) and gains kinetic energy ($KE$) as it moves from A to B. Conservation of energy requires:

$$\begin{split}\big(\text{PE lost}\big) &= \big(\text{KE gained}\big) \\ Mgh &= Mgs\ (\sin\theta) \\\end{split}$$

Ignoring friction this becomes the $KE$ of the cylinder where the total $KE$ is:

$$KE = \big(\text{linear KE }\big)+\big(\text{rotational KE}\big)$$

Therefore:

$$\begin{split}Mgs\ (\sin\theta) &= \frac{1}{2}Mv^2+\frac{1}{2}I\omega ^2 \\\end{split}$$

Substitute $v^2 = 2as$ and $\omega = \frac{v}{r_a}$ :

$$a = \left(\frac{Mgr_a^2}{Mr_a^2 + I}\right) \sin\theta \tag{check this yourself!}$$

Analysis

1. Plot a graph of $a$ against $\sin\theta$ for each cylinder on the same sheet of graph paper. Find the gradient of each line.
2. Given that $a=\left(\frac{Mgr_a^2}{Mr_a^2 + I}\right)\sin\theta$, find $I$ for each cylinder.
3. From theory $I = \frac{1}{2}Mr^2$ where $r = \text{cylinder radius}$. Calculate $I$ using this to check your value from 2 above. Give the % error for your value from 2.
4. If $I = Mk$, find the radius of gyration, $k$, for each cylinder.
5. Calculate the torque necessary to steadily accelerate each cylinder from rest to an angular velocity of $30\text{rad/s}$ in $2\text{s}$.